Tværbelastet polygonal væg

Dette modul beregner en tværbelastet væg efter EN 1996-1-1. Væggen har form som en konveks polygon med højst 10 sider, og hver af væggens rande kan være enten

• fri
• simpelt understøttet eller
• indspændt

Væggen er ikke understøttet andre steder end langs randene.

Væggen kan have én eller flere åbninger (vinduer, døre).

Beregningsmetode

Væggen beregnes efter brudlinieteorien for et anisotropt materiale. Den opdeles i et antal delområder svarende til antallet af simpelt understøttede eller indspændte rande. Hver af disse rande danner den ene side i et delområde, og delområderne er i øvrigt begrænset af og adskilt fra hinanden af rette brudlinier.

Programmet danner på grundlag af tilfældige tal en serie geometrisk tilladelige brudfigurer med denne konfiguration, og beregner bæreevnen for hver brudfigur ved at sætte det indre arbejde ved en bestemt lille deformation lig med det ydre arbejde.

Efter et vist antal beregninger udvælges den laveste af de fundne bæreevner, og den tilhørende brudfigur danner nu udgangspunkt for den næste serie tilfældige brudfigurer, som har et mindre variationsområde end den første serie. Således fortsættes, indtil det på forhånd specificerede totale antal beregninger er foretaget. Den mindste af de fundne bæreevner antages da at være væggens tværbæreevne.

Begrænsninger

I EN 1996-1-1 er der ikke begrænsninger for bøjningsvirkningen i en muret væg i de tilfælde, hvor bæreevnen alene baseres på bøjningstrækspændinger i liggefuger.

Forsvarligheden af at anvende brudlinieteorien på en given væg, må vurderes af en kvalificeret statiker i hvert enkelt tilfælde. Nedenstående eksempler antyder nogle af de overvejelser, statikeren må gøre sig.

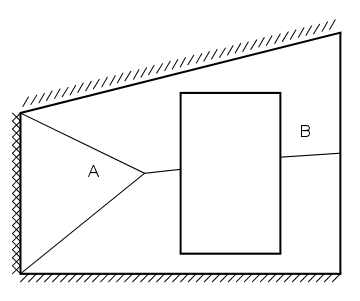
Figur 1. En åbning, der er gennemgående i stort set hele højden

Vægfelt B vil i det viste tilfælde stort set basere sin bæreevne på bøjningstrækspændinger i liggefuger, idet den stabiliserende effekt af den venstre understøttende væg (A) vil være minimal. Såfremt dette ikke ønskes, må størrelsen af vægfelt B i forhold til vægfelt A vurderes.

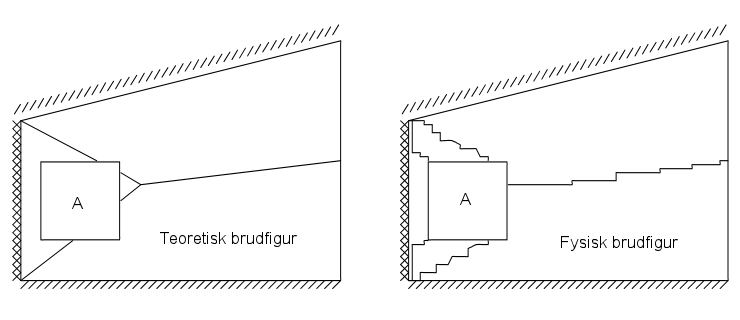
Figur 2. En åbning placeret nær en indspændt rand

Ved en teoretisk beregning vil hele den indspændte venstre rand af væggen blive regnet som en brudlinie og således bidrage til væggens bæreevne. I virkeligheden vil den aktive brudlinie langs den lodrette rand blive en del kortere som antydet på figuren til højre, og dermed vil bæreevnen blive mindre.

Man kan i nogen grad tage hensyn hertil ved at forlænge åbning A, så den når helt ud til indspændingen, og eventuelt også skønsmæssigt forlænge den lidt i den anden ende.

 

Karakteristisk eller deklareret bøjningstrækstyrke i vandret snit

Den bøjningstrækstyrke, der er aktuel ved bøjning om en vandret akse. Hvis bagvægsmaterialet er sat til Murværk på fanebladet "Fællesinformation", overføres værdien f_xk1 automatisk fra fanebladet "Murværk", ellers overføres værdien f_cflk fra fanebladet "Letbeton".

 

Karakteristisk eller deklareret bøjningstrækstyrke i lodret snit

Den bøjningstrækstyrke, der er aktuel ved bøjning om en lodret akse. Hvis bagvægsmaterialet er sat til Murværk på fanebladet "Fællesinformation", overføres værdien f_xk2 automatisk fra fanebladet "Murværk", ellers overføres værdien f_xk2 fra fanebladet "Letbeton".

Hvis væggen opbygges af smalle porebetonelementer, bør bøjningstrækstyrken i et lodret snit i henhold til sædvanlig praksis ikke sættes større end 0,50 MPa. Herved tages højde for eventuelle svagheder i udførelsen af de lodrette fuger.

 

Regningsmæssig tværlast

Den vandrette, jævnt fordelte last vinkelret på væggens plan.

Den samlede regningsmæssige tværlast på væggen fås normalt fra modulet Lastberegning.

Tværlasten angives altid som et positivt tal, uafhængigt af retningen.

For en kombinationsvæg (herunder en hul mur) fordeles den samlede vandrette last på de to vanger efter deres stivheder. Denne beregning udføres af modulet Kombinationsvæg, hvis resultat blandt andet er tværlasten på hver vange.

Lasten kan tillige fordeles efter delvæggenes kapaciteter, såfremt disse er af samme materiale. Fx tegl - tegl eller porebeton - porebeton.

Lasten på vandrette og lodrette understøtninger kan bestemmes ud fra brudliniefiguren. Dvs lastfordelingen svarer så nogenlunde til de felter understøtningen er i forbindelse med (Husk en stålsøjle vil således typisk have 2 x trekantformig last stammende fra vægfelterne den understøtter

Der er i denne version ikke mulighed for at påføre andre laster, såsom lodret last eller randmomenter, på en ikke-rektangulær væg.

Punktlaster vinkelret på vægplanen, fx fra ankre til ophængning af altaner kan ikke regnes via programmet. Dette forhold analyseres fx via lærebogen på www.mur-tag.dk

 

Regningsmæssig tykkelse

Værdien overføres automatisk fra fanebladet "Murværk" eller fra fanebladet "Letbeton", men kan overskrives for den aktuelle komponent.

Den regningsmæssige tykkelse sættes normalt lig den nominelle vægtykkelse. Men hvis der er tale om en muret væg med projekterede tilbageliggende fuger, skal tykkelsen reduceres med den aktuelle fugedybde.

Det sikres, at tykkelsen overholder eventuelle minimumskrav angivet i det nationale anneks N.A. (ikke aktuelt for DK)

 

Vægmateriale

Væggens bæreevne beregnes efter samme metode (brudlinieteorien), uafhængigt af vægmaterialet. Når vægmaterialet alligevel skal angives, skyldes det følgende detailforskelle:

Partialkoefficienterne kan være forskellige for murværk og letbetonelementer. For murede vægges vedkommende bestemmer programmet f_xd1 og f_xd2 ved division af de karakteristiske bøjningsstyrker f_xk1 og f_xk2 med den ene partialkoefficient. For porebetonelementvægges vedkommende bestemmer programmet tilsvarende f_xd1 og f_xd2 ved division af de deklarerede bøjningsstyrker f_cflk og f_xk2 med den anden partialkoefficient.

For porebetonelementvægges vedkommende tages der i henhold til sædvanlig praksis højde for eventuelle svagheder i udførelsen af de lodrette fuger ved at sætte bøjningstrækstyrken om en lodret (vertikal) akse ret lavt. Den hyppigt anvendte "deklarerede" værdi er f_tvg = 0,5 MPa.

 

Definér en ny polygonside

Væggens form skal danne en konveks polygon, dvs en trekant, firkant, femkant, ... eller tikant, hvor alle hjørner er "udadgående". Polygonen skal have mindst 3 og højst 10 sider.

Væggens form defineres gennem en tabel med hjørnepunkternes koordinater og de mellemliggende siders understøtninger. Et af hjørnepunkterne er startpunkt og har pr. definition koordinaterne (0,0). De øvrige punkters koordinater angives således i forhold til startpunktet. Disse koordinater skal angives i meter og i rækkefølge med uret. Da polygonen også skal være konveks, skal man altså "dreje til højre" i hvert hjørne.

Figur 3. Definition af polygon

En linie i den nævnte tabel skal indeholde et hjørnepunkts koordinater i m og understøtningsformen for den side, der går fra det forrige punkt til det aktuelle. Den første linie i listen skal derfor indeholde koordinaterne til det første punkt efter startpunktet og understøtningsformen for siden fra startpunktet til det første punkt efter startpunktet. Den sidste linie i listen skal indeholde koordinaterne til startpunktet (0,0) og understøtningsformen for den sidste side frem til startpunktet.

En ny side tilføjes ved at tilføje en ny linie i tabellen. Dette gøres ved at trykke på en grøn knap med et "ny linie"-symbol ude til højre. En forkert linie kan slettes ved at trykke på den røde knap med krydset til højre for linien.

Der kan vælges mellem følgende understøtningstyper:

• fri
• simpelt understøttet
• indspændt

Fri betyder, at siden slet ikke er, eller ikke kan regnes, understøttet. En side kan regnes understøttet, hvis en tværgående væg, søjle eller lignende er i stand til, at optage det aktuelle vægfelts reaktioner uden væsentlige differensbevægelser. For en formurs vedkommende overføres reaktionen til den bagvedliggende konstruktion gennem en binderrække.

En side kan regnes indspændt, hvis siden er understøttet og et tilstødende vægfelt er i stand til at optage et moment svarende til det aktuelle vægfelts brudmoment. Dette er for eksempel tilfældet, hvis det aktuelle ydervægsfelt fortsætter i et naboydervægsfelt uden store åbninger i nærheden af skillelinien.

En understøttet side, som ikke er indspændt, er simpelt understøttet.

 

Definér en ny muråbning

Åbninger defineres gennem en tabel med åbningernes form, placering og dimensioner.

En ny åbning tilføjes ved at tilføje en ny linie i tabellen. Dette gøres ved at trykke på en grøn knap med et "ny linie"-symbol ude til højre. En forkert linie kan slettes ved at trykke på den røde knap med krydset til højre for linien.

En muråbnings form kan være én af følgende tre:

• Rektangel
• Ruder
• Ellipse

Ruderformen er en firkant med et hjørne der vender opad, et der vender nedad, et der vender til venstre og et der vender til højre. De fire sider er lige lange og danner alle den samme vinkel med vandret, bortset fra fortegnet. Formen er altså symmetrisk både om en lodret og en vandret linie.

For alle tre typer gælder det, at åbningens placering angives ved koordinaterne X og Y (den vandrette og lodrette afstand fra væggens nederste venstre hjørne) til åbningens referencepunkt R. Referencepunktet for en rektangulær åbning er åbningens nederste venstre hjørne. Referencepunktet for en ruderformet eller en ellipseformet åbning er det nederste venstre hjørne af det omskrevne rektangel, se figuren.

Åbningens størrelse angives ved bredden B og højden H. For en ruderformet eller en ellipseformet åbning angives bredden og højden af det omskrevne rektangel, se figuren.

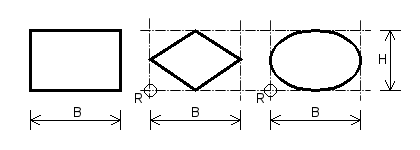
Figur 4. Åbninger

Åbninger kan kombineres ved overlapning, sådan at mere komplicerede former kan angives.

Geometrien for væggen og dens åbninger må vurderes af en kvalificeret statiker i hvert enkelt tilfælde.

---