Teglbjælker

Programmet beregner teglbjælker efter beregningsregler angivet i EN 1996-1-1. Beregningsreglerne er verificeret ved hjælp af nye og tidligere udførte danske forsøg med teglbjælker. Korrelationen mellem beregningsmodellen og forsøgsresultaterne er god, såfremt realistiske, differentierede materialeparametre anvendes (f.eks. materialemodellerne beskrevet i pjecen TEGL 24). Det danske forsøgsmateriale består af mere end 100 teglbjælker med varierende parametre.

Den effektive bjælkelængde regnes som lysningsvidden + minimum(vederlagslængden eller den effektive højde). Forskydningskraften bestemmes, iht EN 1996-1-1, i afstanden ½ * den effektive højde fra lysningsviddens start. Derfor bliver forskydningskraften svagt mindre end reaktionen. Kohæsionen kan forøges såfremt forholdet mellem forskydningsspændvidden (a_v) og den effektive højde (d) er mindre end 2 dvs (a_v/d < 2). Kohæsionen kan forøges med en faktor (max(4, 2d/a_v)). Forøges kohæsionen skal forskydningskraften dog bestemmes ved lysningsviddens start. Dvs for asymmetriske belastninger kan forskydningskapaciteten være forskellig for højre og venstre side.

Der er endvidere indført et bæreevnekriterie mht. tøjningen i trækzonen i den midterste del af bjælken. Træktøjningen i nederste liggefuge skal være mindre end 0.5 o/oo for at bæreevnen vurderes som tilstrækkelig. Forsøg på Teknologisk Institut, Murværk har vist, at denne værdi er på den sikre side for normalt anvendte bjælker.

Beregningsmodellen er kun relevant for normalt armerede tværsnit, hvilket er den normalt forekommende situation for teglbjælker. Men er bjælken lav og kraftig armeret bliver momentbæreevnen undervurderet. I sådanne (sjældne tilfælde) regnes med et lavere antal aktive armeringsstænger end det aktuelt forekomne.

Indspændingsmoment.
Det skal naturligvis sikres, at den til teglbjælken tilstødende konstruktion er i stand til at optage det aktuelle moment, der skal overføres fra en eventuel indspænding (ved anvendelse af toparmering).

Indspændingsmomentet ved enderne regnes ikke større end halvdelen af det faktiske postive moment når bjælken betragtes som simpelt understøttet, også selvom momentkapaciteten ved enderne er større.

 

Karakteristisk kohæsion f_vk0

Kohæsionen f_vk0 er den del af forskydningsstyrken, der ikke stammer fra friktionen.
Værdien overføres automatisk fra fanebladet Murværk.

Værdien kan naturligvis overskrives i den aktuelle beregning.

For præfabrikerede teglbjælker (dvs teglbjælker på 3 eller flere skifter) anvendes typisk en værdi for f_vk0 som er væsentlig højere end for in-situ muret teglbjælker. Værdierne er bestemt via forsøg for de enkelte bjælkeproducenter. Værdierne for f_vk0 kan ligge i området (0,60 MPa - 0,80 MPa)

Ved indlæggelse af TB-rende bør kohæsionen reduceres svarende til en reduktion i tykkelsen på 10 mm.
Dvs ved anvendelse af 108 mm bjælker, bør kohæsionen reduceres en faktor 98/108 = 0,91

 

Armeringsdiameter i bund

Indstøbt armering i en tegloverligger har ofte diameteren
5 mm ved forspændt armering
8 mm ved slap armering
men også andre dimensioner anvendes.

Armeringssystemer til indlæggelse i liggefugen har ofte diameteren 3 - 5 mm.

Såfremt tegloverliggeren er bredere end den overliggende murværk (se efterfølgende figur) vil den kombinerede teglbjælke have tendens til at bøje ud af planen ved kraftig belastning. Asymmetriforholdene gør endvidere, at ikke al armeringen kan regnes effektiv.

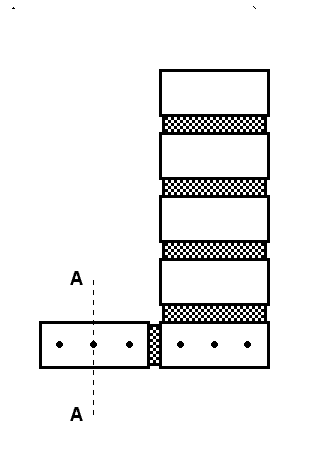
Figur 1. L - formig teglbjælke

Ved angivelse af armeringsantallet bør kun halvdelen af den armering, der ligger uden for konturerne af den samlede bjælke medtages. I figuren svarer dette til line A - A

 

Armeringsdiameter i top

Armeringssystemer til indlæggelse i liggefugen har ofte diameteren 3 - 5 mm.

 

Karakteristisk elasticitetsmodul E_0k

Værdier overføres automatisk fra faneblad Murværk.

Værdien kan naturligvis overskrives i den aktuelle beregning.

 

Enkeltkræfter, teglbjælker

Enkeltkraftens regningsmæssige værdi. Der kan regnes med vilkårligt mange enkeltkræfter.

 

Karakteristisk basistrykstyrke f_k

Værdien overføres automatisk fra fanebladet Murværk.

Værdien kan naturligvis overskrives i den aktuelle beregning.

 

Forspændt

Forspændt eller slap armering.
Den forspændte armering giver større stivhed og dermed mindre nedbøjning.
Den regningsmæssige bæreevne er stort set den samme for den slapt armerede og den forspændte teglbjælke.
Forspændingen skal foretages som beskrevet i DMUK's produkt bestemmelser.

   

Flydespænding f_yk og E-modul E_0k

Armeringsstål til tegloverliggere skal være ribbestål eller stål med overfladeprofilering.

Armeringsstål til tegloverliggere i formure og i vægge omkring vådrum skal være korrosionsfast, f.eks. rustfast stål iht. "DS/INF 167 til EN 1996-2".

Armeringsstål til tegloverliggere i bagmure og i vægge mellem tørre rum er normalt almindeligt tentorstål eller kamstål.

fyk er den karakteristiske flydespænding eller 0,2%-spænding. For tentorstål kan den normalt antages at være 550 MPa og for kamstål 420 MPa. For korrosionsfast stål forekommer forskellige værdier; spørg den aktuelle leverandør, eller se under www.mur-tag.dk.

Det karakteristiske E-modul for armeringsstål kan normalt antages at være 200.000 MPa.

 

Bjælkehøjde

Bjælkehøjden inkl. tegloverliggeren, målt i mm. Det er afgørende vigtigt, at de skifter der medregnes til bjælkehøjden, er effektivt sammenhængende over hele bjælkelængden.

Bjælkehøjden vil typisk kunne regnes fra undersiden af tegloverliggeren til papindlægget.

  

Toparmering ved understøtning

Momentbæreevnen kan forøges ved at indlægge toparmering i venstre/højre side, hvorved bjælken indspændes

 

Højde til armeringens tyngdepunkt

Højde fra lysningsoverkant til armeringstyngdepunkt. Hvis armeringen ligger i ét lag, indstøbt i udfræsninger i en tegloverligger, sættes højden normalt til 30 mm.

Nyttehøjden (h_e) sættes af programmet til den totale bjælkehøjde minus højden til armeringens tyngdepunkt minus 20 mm. Med de 20 mm tages der hensyn til, at den øverste fuge ved paplaget ikke kan medregnes til bjælken og placeringstolerancer.

 

Højde til armeringens tyngdepunkt, toparmering

Denne værdi er typisk et helt antal skifter fra overkant af bjælke til armeringen.

 

Lysningsvidde

Regningsmæssig bredde af åbningen under teglbjælken.

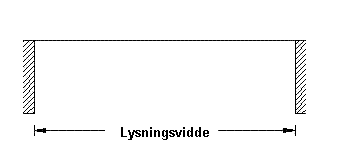
Figur 2. Lysningsbredde

Ofte lig med bredden af åbningen, men ved projekterede tilbageliggende fuger, skal lysningsvidden forøges med den aktuelle fugedybde i begge sider.

Det anbefales at kontrollere teglbjælkens dimensioner og eventuelle enkeltkræfters placeringer for grove fejl ved hjælp af knappen "Tegning".

 

Regningsmæssig murtykkelse

Ved projekterede fugedybder skal tykkelsen reduceres med den aktuelle fugedybde.

Eksempel:
Udføres murværket i byggesten med bredden 168 mm og med 10 mm ensidigt tilbageliggende fuge fås murtykkelsen til: 168 mm - 10 mm = 158 mm.

Det sikres, at tykkelsen overholder eventuelle minimumskrav angivet i det nationale anneks N.A. (ikke aktuelt for DK)

 

Antal armeringstråde i bund

I en tegloverligger er antallet af armeringstråde/stænger ofte:
108 mm bred overligger: 2 tråde
168 mm bred overligger: 3 tråde
200 mm bred overligger: 4 tråde

Ved armering i liggefugerne skal den fri afstand mellem armeringsstænger være mindst to gange diameteren.

 

Antal armeringstråde i top

Ved armering i liggefugerne skal den fri afstand mellem armeringsstænger være mindst to gange diameteren.

Armeringssystemer har oftest 2 tråde.

 

Lodret linielast

Bjælkens regningsmæssige linielast kan stamme fra egenlast af murværket i og over bjælken og fra egen- og nyttelast på etageadskillelser.

Lasthøjde for teglbjælker:

Den ensfordelte last på teglbjælker stammende fra overliggende murværk kan bestemmes ud fra følgende regler, hvor der tages hensyn til, at der i det overliggende murværk dannes en ”skjult” bue, som fører kræfterne uden om den aktuelle teglbjælke.

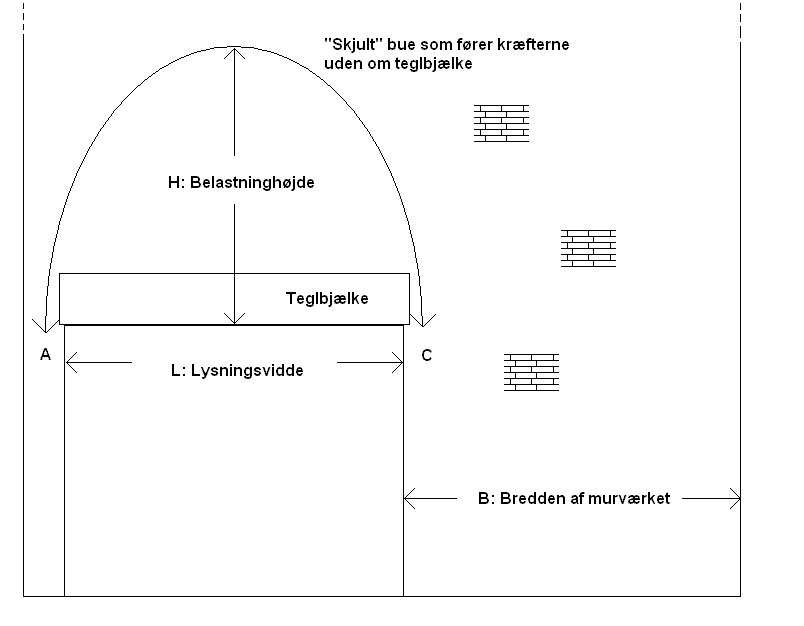
Figur 3. Illustration af lastoptagelse ved teglbjælke

Fælles for situation I og II

Teglbjælken skal optage lasten under buen, som er parabel-formet. Da det er praktisk vanskelig at regne med denne lasttype, antages konservativt, at lasten er ensfordelt med en størrelse svarende til højden af buen.

- Situation I

Smal søjle ved hjørne, dilatationsfuge eller lignende.

Såfremt murværket ved den ene understøtning (på ovenstående figur, benævnt A) er smal og hvor bæreevnen for vandret påvirkning dermed er ringe, kan regnes med en belastningshøjde: H = L.

Uanset hvor stor en andel af den overliggende last, der regnes overført via buevirkning, starter søjlen A’s lastopland midt i lysningen og dækker al det overliggende murværk

- Situation II

Ved begge understøtninger er der stor udstrækning af murværket i vandret retning.

Såfremt murværket ved begge understøtninger har stor udstrækning i vandret retning (B > L) (svarende til siden C på figuren) kan belastningshøjden sættes til: H = L/2 for B > L

- Situation III

Murværket er ophængt på konsoller rundt om hjørnet og understøtning A eksisterer ikke.

I dette tilfælde kan der ikke etableres en bue og al overliggende last må påregnes at påvirke teglbjælken.

Bemærk:

Såfremt vinduer er forskudt i vandret plan mellem etager og dermed ikke ligger over hinanden, kan den lodrette last på teglbjælken blive særdeles stor og i nogen tilfælde svare til hele facadens last".

 

Vederlagslængde u

Eksempel 1:
Teglbjælken er udført med en præfabrikeret tegloverligger, der er understøttet af murværk i bjælkens eget plan. Vederlagslængden u sættes lig med eller mindre end tegloverliggerens fysiske vederlagslængde, som skal være mellem 108 mm og 348 mm.

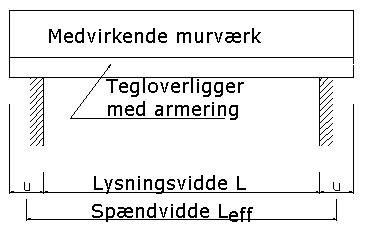
Figur 4. Vederlag. Overligger

Vederlag for ”let last” (fx egenvægt af overliggende murværk)

• Åbning 0.0 m - 1.2 m. Vederlag: ½ sten
• Åbning 1.2 m - 1.8 m. Vederlag: 3/4 sten
• Åbning 1.8 m - 3,0 m. Vederlag: 1 sten
• Åbning 3,0 m - Vederlag: 1½ sten

For tung last bør vederlaget forøges. Dog anvendes maksimalt 1½ stens vederlag.

Eksempel 2:
Teglbjælken er udført ved indmuring af et præfabrikeret armeringssystem i en eller flere liggefuger. Vederlagslængden u sættes lig med eller mindre end den faktiske forankringslængde af armeringsystemet, dog mindst 108 mm. Den faktiske forankringslængde (Lb) skal mindst være den i udskriften angivne forankringslængde.

Figur 5. Vederlag. Armeringssystem

Det anbefales at kontrollere bjælkens dimensioner og eventuelle enkeltkræfters placeringer for grove fejl ved hjælp af knappen "Tegning".

---