Beregning af stabiliserende vægfelter

Modulet beregner stabiliserende vægfelter påvirket af vandrette og lodrette belastninger i eget plan (skiver). Beregning af stabiliserende vægfelter kan være ret omstændig, da det ofte kan være svært at afgøre hvilke vægfelter i en konstruktion, der er kritiske. Endvidere er det ikke umiddelbart logisk, hvor skiven i sig selv har svage punkter. Bruddet kan i modsætning til pladefelter, bjælker, søjler etc. opstå mange forskellige steder i skiven.

En uddybende forklaring på skiver, flanger, beregningsmodel, etc findes i lærebogen del 2, afsnit 5.3. Se: www.mur-tag.dk

Efterfølgende er angivet, hvorledes belastningerne på væggene bestemmes samt beregningsmodellen for modulet.

Bestemmelse af belastninger:
Kritiske vægfelter udvælges.
Bygningen betragtes som en indspændt bjælkesøjle påvirket af max. vind og min. egenvægt.
Snitkræfterne M og Q umiddelbart over den aktuelle væg bestemmes vha. ligevægtsligningerne.
De fundne værdier for M og Q fordeles efter stivhederne på de aktuelle vægge.
N bestemmes som den væg- og dæklast, der i lodret retning direkte belaster den aktuelle væg.

Beregningsmodel:
Med de inddaterede parametre undersøger modulet bæreevnen efter følgende model:

Forskydningskapaciteten (Q-flange) mellem flanger og vægfelt bestemmes. Kraften regnes overført ved skrå trykstringere og vandrette trækstringere (bindere). Flangernes længde reduceres evt. pga. Q-flange eller for at skabe en spændingsfordeling, som bevirker en begyndende rotation af væggen.
Flangelængden regnes ikke mindre end vægtykkelsen.
Lodrette snit gennem væggen er benævnt A, B, C, D:
Det forudsættes at vinden kommer fra venstre.

1. Overgang mellem venstre flange og vægfelt
2. Umiddelbart til venstre for belastningsfladen
3. Umiddelbart til venstre for reaktionsfladen
4. Overgang mellem højre flange og vægfelt

Den vandrette afstand imellem snit B og C er benævnt LBC, osv

Spændingsfordelingen kan have flere forløb:
LBC er forskellen på udstrækningen af spændingsfordelingen i bund og top
e: excentriciteten af reaktionen

Ekstrem : e > L/2. Resultanten falder uden for væggen. Holder ikke. (L er væggens samlede længde)

Bemærk dog: Excentriciteten er begrænset til ikke at må være tættere på kanten end 228 mm, ud fra en overvejelse om, at hele lasten som minimum skal overføres gennem 2 sten, da der muligvis kan være udskæringer til elkabler o.lign. Hvis man regner på andre materialer end teglmursten kan værdien forekomme lidt arbitrær, men skal under alle omstændigheder betragtes som en sikkerhed mod, at kræfterne ikke overføres gennem den alleryderste kant på skiven.

Ovenstående sikrer således, at kræfterne ikke overføres gennem et minimalt murværkstværsnit, hvilket ikke er tillads iht. EN 1996 - 1 - 1.

Normal : LBC > 0. Typisk fordeling.

Lodret : LBC = 0.

Stabil : LBC < 0. Ingen problemer.

Yderst stabil: e < 0. Excentriciteten fra reaktionen modsat W.

For normal og lodret fordeling undersøges konstruktionen i en række snit:

• Ved understøtningen: Normalkraft og glidning. (Vandret snit)
• Snit B. Lodret brud gennem sten. Brud i liggefuge. Træk- og trykstringer. (Lodret snit)
• Snit C. (kun tilfælde: normal). Som ovenstående samt normalspænding. (Lodret snit)
• Liggefuge over trykstringer. Forskydningsspændinger. Strækning AB-BC-CD. (Vandret snit)
• Liggefuge under trækstringer. Som ovenstående samt excentrisk påvirkning. (Vandret snit)
• Belastningsfladen. Normal- og forskydningsspænding. (Vandret snit)

 

Lodret afstand mellem bindere

Afstanden angives i mm.

Der indlægges typisk bindere i hver 2. eller 4. fuge, således at indmuringen i fortandingen foregår ved, at der påmures "oven" på den indlagte binder. Forskydningskraften mellem flanger og den stabiliserende væg regnes overført vha. et stringersystem bestående af skrå trykstringere under 45° mellem binderne samt vandrette trækstringere i binderne.

Længden på binderne skal derfor minimum være lig den lodrette afstand mellem binderne.

   

Densitet

Egenvægten af væggen indgår som en del af den regningsmæssige lodrette stabiliserende last.

Såfremt der regnes med en partialkoefficient mindre end 1,0 på denne værdi, skal dette inkluderes i værdien for densiteten.

Murværk af massive sten:

Densiteten er typisk 1700-1800 kg/m³

Murværk af hulsten:

Der kan regnes med følgende værdier:

Hulrum %	Densitet kg/m³
10	1580
15	1510
20	1440
25	1370
30	1300
35	1230
40	1160

Tabellen er udarbejdet under følgende forudsætninger:

Densitet af teglmateriale:	1800 kg/m³
Stenandel:	78,4 %
Densitet af fugemørtel:	1700 kg/m³
Fugeandel:	21,6 %
Hulrum i fuger:	15 %

Korrektioner:

Klinkbrændte sten kan have densiteter større end 2000 kg/m³.

Molersten har densitet 500-800 kg/m³.

I flere moduler bestemmes væggens egenlast pr. m² vægflade som densiteten gange vægtykkelsen. Hvis et evt. pudslag ønskes medregnet til egenlasten, må densiteten sættes tilsvarende højere, idet vægtykkelsen af hensyn til bæreevnen ikke må angives med en for stor værdi.

 

Excentricitet e₀

Excentriciteten af den lodrette last, vinkelret på vægplanet, ved væggens overside beregnes som beskrevet i DS/INF 167 til EN 1996-1-1. Hver enkelt lodret dellast sammen med sin egenexcentricitet giver et bidrag til den resulterende last og den resulterende excentricitet, og den enkelte dellasts excentricitet skal antages "størst mulig" eller "mindst mulig", afhængigt af, hvad der giver den største totale excentricitet.

En stabiliserende væg regnes ikke påvirket af tværlaster, hvilket medfører, at excentricitetens retning er underordnet, idet væggen er symmetrisk om eget plan.

I praksis er væggen naturligvis påvirket af en vindlast, som medfører en sædvanlig momentspændingsfordeling parallel med ligge- og studsfuger. Denne spændingsfordeling giver, i den trykpåvirkede halvdel af fx liggefugen, et ekstra bidrag til forskydningskapaciteten på +µ_d * σ. I den trækpåvirkede halvdel formindskes forskydningskapaciteten tilsvarende med -µ_d * σ. Bidraget er således negligibelt

Her er σ tryknormalspændingen.

Den vandrette last regnes at have samme excentricitet som den lodrette. Dette er på den sikre side, da en del af de vandrette kræfter i realiteten overføres gennem det ubelastede tværsnit. For ensidigt oplagte dæk bestemmes e₀ til:
e₀ = t/2 - a₁/3
hvor t er vægtykkelsen og a₁ er oplægningsdybden.

 

Excentricitet i væggens plan e_L

Vindlasten giver anledning til et samlet moment, som konstruktionen i ethvert snit skal kunne optage.
Momentet fordeles efter stivhederne af tværvæggene.
Momentet giver en excentricitet af normalkraften i væggens plan.
Excentriciteten bestemmes af e_L = M/N

For vægge i øverste etage er e_L normalt lig 0

 

Karakteristisk basistrykstyrke f_k

Værdien overføres automatisk fra fanebladet Murværk.

Værdien kan naturligvis overskrives i den aktuelle beregning.

  

Excentricitet e₀ ved flanger

Den lodrette lasts excentricitet ved væggens overside. Beregnes som beskrevet i I DS/INF 167 til EN 1996-1-1. Et af de centrale principper i denne beregning er, at hver enkelt lodret dellast sammen med sin egen excentricitet giver et bidrag til den resulterende last og den resulterende excentricitet, og at den enkelte dellasts excentricitet skal antages "størst mulig" eller "mindst mulig", afhængig af, hvad der giver den største totale excentricitet.

For ensidigt oplagte dæk bestemmes e₀ til:
e₀ = t/2 - a₁/3
hvor t er vægtykkelsen og a₁ er oplægningsdybden.

I øvrigt har excentriciteten på flangernes lodrette last kun ringe betydning for bæreevnen af det stabiliserende vægfelt.

    

Udstrækning af flanger

Her angives den maksimale afstand fra væggens symmetrilinie til nærmeste fri kant eller større muråbning.
Ved større muråbning forstås her en åbning hvor:
h > 1/4 * etagehøjden eller
b > 1/4 * længden af vægfeltet
hvor h, b er muråbningens højde og bredde

I mange tilfælde kan bæreevnen ikke forøges ved at angive en udstrækning for højre flange. Dette skyldes, at denne flange kun kan overføre lodret kraft (og ikke vandret) og dermed vil friktionsbidraget (og dermed den samlede bæreevne) reduceres.

  

Lodret last på højre flange

Lasten på højre flange har kun ringe indflydelse på bæreevnen af det stabiliserende vægfelt. Dette skyldes, at lasten hovedsagelig forsætter gennem flangen ned i understøtningen.
Lasten på den højre flange og rumvægten kan udmærket sættes = 0, ud fra følgende betragtninger.

Tværgående skillevægge opmures typisk efter dækkene er placeret på de langsgående vægge. Herved er den for kraftoptagelsen nødvendige tøjning i de langsgående vægge fremkommet, og en opmuring af de tværgående vægge ændrer ikke synderligt på dette forhold.

Dvs at de lodrette laster optages direkte igennem de langsgående vægge og er i realiteten forskydningsoptagelsen uvedkommende. En begyndende rotation af det stabiliserende vægfelt vil derimod fremkalde en tøjning i flangen og dermed en stabiliserende forskydningskraft i samlingen mellem flange og vægfelt.

Lodret last på venstre flange

Vægskiven vil under den begyndende rotation forsøge at "løfte" venstre flange, hvilket rent statisk betyder, at der fremkommer en stabiliserende forskydningskraft på vægfeltet. For vægskiven på den overliggende etage opstår de samme mekanismer, hvilket medfører, at den eneste last, den aktuelle vægs skive kan regnes påvirket af ved "løftet", er flangens egenvægt samt dæklasten på den overliggende etage.

I øvrigt er væggens forskydningskapacitet ofte dimensionsgivende, således at en kraftigere belastning af flangen blot vil betyde, at flangen, under beregningen, vil blive reduceret tilsvarende.

   

Regningsmæssig murtykkelse

For mursten i dansk normal- eller bredstensformat er tykkelsen hhv. 108 eller 168 mm. Ved projekterede fugedybder reduceres tykkelsen med den aktuelle fugedybde.

Eksempel:

Udføres murværket med byggesten med en bredde på 168 mm og med 10 mm ensidigt tilbageliggende fuge fås den regningsmæssige murtykkelse til: 168 mm - 10 mm = 158 mm.

Det sikres, at tykkelsen overholder eventuelle minimumskrav angivet i det nationale anneks N.A. (ikke aktuelt for DK)

 

Karakteristisk forankringsstyrke for bindere

Forskydningskraften mellem flanger og den stabiliserende væg regnes overført vha. et stringersystem bestående af skrå trykstringere under 45 grader mellem bindere samt vandrette trækstringere i binderne.

Trækstyrken i binderne sættes lig forankringsstyrken.

Værdien overføres automatisk fra fanebladet Murværk.

Værdien kan naturligvis overskrives i den aktuelle beregning.

I nedenstående tabel er de karakteristiske forankringsstyrker angivet for Ø3 og Ø4 mm Z-bindere med min. 50 mm ombuk og 40 mm indmuringslængde (målt fra begge sider).

Tabel. Karakteristiske forankringsstyrker i kN for Z-bindere indmuret i murværk

Mørtlens trykstyrke	Ø4 bindere	Ø3 bindere
20	5,0	2,5
10	3,5	1,8
5	2,5	1,3
2,5	1,8	0,9
1,5	1,5	0,7

For murværk med f_xk1 < 0,25 MPa skal forankringsstyrkerne for Ø4 bindere reduceres med 20%.

Såfremt indmuringslængden er mindre end 40 mm kan regnes med lineært aftagende forankringsstyrke til 0 kN gældende for 20 mm.

Dvs ved 30 mm indmuringslængde er forankringsstyrken halveret.

 

Karakteristisk friktionskoefficient µ_k

Friktionen µ_k er den del af forskydningsstyrken, der ikke stammer fra kohæsionen. Værdien overføres automatisk fra fanebladet Murværk.

Værdien kan naturligvis overskrives i den aktuelle beregning.

 

Karakteristisk friktionskoefficient ved bund

Følgende karakteristiske friktionskoefficienter (µ_k,bund) kan anvendes for friktion mod fugtspærre:

Fundament	Fugtspærre: Pap
Glat	0,49
Letklinkerbeton	0,44
Kostet	0,31

Fundament	Fugtspærre: Plastfolie
Glat	-
Letklinkerbeton	0,62
Kostet	-

I DS/INF 167 til EN 1996-1-1 er µ_k,bund sat til 0,4.

 

Højde

Hvis vægfeltet står på et dæk eller et fundament, måles den regningsmæssige højde fra dækkets eller fundamentets overside. Er der indlagt murpap f.eks. 2 skifter over fundamentet, regnes højden dog herfra.

Hvis vægfeltet er fastholdt af et dæk, som hviler på væggens overside, måles den regningsmæssige højde til undersiden af dækket.

 

Forskydningsfaktor k_m

Forskydningsstyrken for byggesten regnes proportional med sten- eller bloktrykstyrken. Såfremt der ikke foreligger forsøgsresultater eller anden form for dokumentation, kan følgende regningsmæssige værdier anvendes.

k_m = 0,07 for tegl
k_m = 0,20 for letbetonblokke/plader  

Karakteristisk kohæsion f_vk0

Kohæsionen f_vk0 er den del af forskydningsstyrken, der ikke stammer fra friktionen. Værdien overføres automatisk fra fanebladet Murværk.

Værdien kan naturligvis overskrives i den aktuelle beregning.

 

Karakteristisk kohæsion ved bund

Kohæsionen f_vk0,bund er den del af forskydningsstyrken, der ikke stammer fra friktionen.
f_vk0,bund er sædvanligvis 0 for vægge på fugtspærre.

Såfremt der anvendes en samling bestående af limmørtel - pap - limmørtel, kan der normalt regnes med en kohæsion på 0,20 MPa. Det skal dog samtidig sikres, at forankringen for væltning er tilstrækkelig og funktionel uden rotation af vægfeltet. Dvs forankringen skal være indstøbt og/eller kraftig opspændt. Der bør højst regnes med en flydespænding på: fyk = 200 MPa i forankringsstængerne for at sikre, at kohæsionssamlingen forbliver intakt.

 

Længde

Væggen skal i den angivne længde være opmuret uden stående fortanding, dilatationsfuger og være uden muråbninger (ved enderne forudsættes en fri kant eller stående fortanding).

 

Studsfuger i hvert n. skifte

Den lodrette forskydningskapacitet bliver bestemt i det snit, som passerer det størst mulige antal studsfuger.
For at kunne beregne det aktive tværsnit, angives afstanden mellem studsfuger der ligger over hinanden, som et antal skifter.

Følgende værdier for n kan typisk anvendes:

n	Forbandttype
2	¼ stens løberforbandt
2	½ stensløberforbandt
2	Løberforbandt I
4	Løberforbandt II
2	Munkeforbandt
2	Krydsforbandt
2	Blokforbandt

 

Lodret last

Den regningsmæssige lodrette last er summen af regningsmæssige laster fra overliggende dæk, etc., som direkte påvirker vægfeltet. Den lodrette last virker som regel til gunst for stabiliteten. Den lodrette last påsættes i toppen, som en enkeltkraft i angrebslinien.

 

Vandret last

Den totale vandrette vind- eller masselast fordeles på de stabiliserende vægge efter stivhederne.

Der er ikke mulighed for at påsætte en jævn fordelt, vandret last på venstre lodrette kant. Halvdelen af en sådan last kan evt. inkluderes i den vandrette last i toppen. Den resterende last kan regnes at angribe i bunden og angives ikke. Såfremt glidning er kritisk, regnes hele lasten at angribe i toppen.

 

Trækstringerens kapacitet

For at der kan skabes ligevægt i et forskydningsfelt for de i praksis forekomne påvirkninger, skal der indlægges en trækstringer i oversiden.

Trækstringeren kan f.eks. bestå af fx fugearmering i dækudstøbning, indlagt armering i fugerne eller murværkets egen trækkapacitet.

Stigarmering

Trækkapaciteten for stigarmering kan fx være:

T_Ed= 2 × (pi/4) × 3,7² × 775 MPa / 1,2

T_Ed= 11 kN

Trærem:

En trækstringer kan ikke bestå af en trærem sømmet ned i fx en porebetonvæg.

En trækstringer kan muligvis bestå af en trærem skruet ned i fx en teglstensvæg. Det skal dog eftervises, at trækket kan overføres gennem de aktuelle skruer over en vis strækning. Dette er illustreret på efterfølgende skitse. Den angivne kapacitet af trækstringeren bør ikke angives større end skruernes samlede regningsmæssige udtræksstyrke over 1 - 2 m i længden.

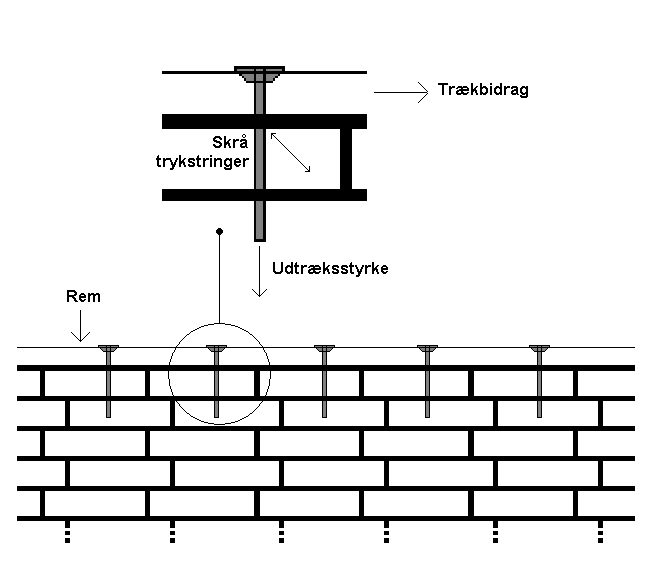
Figur 1. Teglvæg - trærems - løsning

Armering:

Eksempel:
Som dækudstøbning er placeret 1 stk 8 mm armering med fyd = 161 MPa. I øverste fuge er placeret 2 x 5 mm armeringssystem med fyd = 464 MPa.

Heraf fås T_s = pi/4 x (2 x 5² x 464 + 8² x 161)/1000 = 26,31 kN

Murværkets egen trækstyrke:

Er der ingen trækstringer indlagt, kan murværkets egen trækkapacitet for de øverste 5 skifter skønnes. Denne værdi er afhængig af forbandttypen, forskydningsstyrken og trækstyrken af stenene.

Nedenstående udtryk kan anvendes:

T_s = Minimum ((0,14 x kvrod(stentrykstyrken) x h x b x n), (µ_d x σ + f_vd0) x b x σ_l))

hvor 0,14 x kvrod(stentrykstyrken) repræsenterer stenenes trækstyrke
h, b er højden og bredden på de anvendte sten
n er antallet af sten i det snit som passerer det størst mulige antal studsfuger (i de 5 øverste skifter)
µ_d, σ er den regningsmæssige friktion og normalspændingen i skifterne
f_vd0 er den regningsmæssige kohæsion
σ_l er den mindste samlede længde af liggefuger der undergår et forskydningsbrud, når de 5 øverste skifter samlet udsættes for et trækbrud

Første led i udtrykket repræsenterer et trækbrud gennem stenene og studsfugerne. 2. Led repræsenterer et brud alene gennem fugerne. Der regnes ikke med nogen trækkapacitet i studsfugerne. Mindste værdi anvendes.

Et ubelastet (σ = 0) vægfelt med et forbandt med overliggende studsfuger i hvert andet skifte har mindst bæreevne. Her fås, f.eks. med f_b = 10 MPa, f_vd0 = 0,1 MPa, sten i normalformat:

T_s = Minimum(0,14 x kvrod(10) x 55 x 108 x 2, (0,1 x 108 x 228)) = Minimum(5,2 kN, 2,4 kN) = 2,4 kN.
Dvs 2,4 kN kan anvendes som minimumsværdi i alle tilfælde for murværkets egen trækkapacitet.

Porebetons egen trækstyrke:

Er der ingen trækstringer indlagt, kan porebetonens egen trækkapacitet for den øverste del af væggen skønnes.

Denne værdi er afhængig af densiteten, som her forudsættes til minimum 535 kg/m³

Trækstyrken af Porebetonen sættes til 50 % af bøjningstrækstyrken.

Nedenstående udtryk anvendes:

T_s = (t x h x 50 % x f_xd2)

t er tykkelsen og regnes til 100 mm

h er højden af det aktive tværsnit som sættes til 400 mm

Studsfuger regnes limet

f_xd2 er den regningsmæssige bøjningstrækstyrke om en lodret akse og sættes til 0,40 MPa/1,7 = 0,24 MPa

T_s = (100 x 400 x 0,5 x 0,24) = 4,8 kN

Dvs 4,8 kN kan anvendes for porebetonvæggens egen trækkapacitet (med de aktuelle forudsætninger)

 

Stentrykstyrken f_b

Sten- eller bloktrykstyrke for en given stentype opgives af leverandøren.

---