Lodret belastet muret væg (Ritter)

Programmodulet "Lodret belastet muret væg (Ritter)" foretager en bæreevneeftervisning efter Ritter formlen

Ritter formlen er ikke nævnt i EN 1996 – 1 – 1 og er således en dansk alternativ metode, som er angivet i DS/INF 167

Modulet bør anvendes, når den lodrette last i det dimensionsgivende tværsnit er større end 15 % af kapaciteten for den aktuelle væg beregnet som en centralt påvirket søjle

Programmodulet foretager en bæreevneeftervisning for et vægfelt uden åbninger. For en bærende væg med store vinduesåbninger må man derfor beregne hvert vægfelt mellem åbningerne separat. En bærende væg med små vinduesåbninger kan derimod beregnes som en samlet væg. I begge tilfælde må den samlede last på væggen naturligvis fordeles over væggens effektive længde, dvs summen af længderne af de enkelte vægfelter mellem åbningerne. Der kan jo ikke overføres lodret last gennem en vinduesåbning.

Da lasten er en kombination af lodret last, tværlast og excentricitetsmomenter, er bæreevnen ikke blot et enkelt tal. Programmet foretager bæreevneeftervisningen på den måde, at det konstruerer et n-m-diagram for den givne væg, og sammenligner den givne lastkombination med diagrammet.

Et N-M-diagram for en søjle viser sammenhængen mellem den aktuelle lodrette last på søjlen og det moment, der samtidig kan optages. En søjle i et materiale uden trækmodstand kan ikke optage noget moment uden at der samtidig optræder en vis lodret last, der kan stabilisere søjlen. Men der er naturligvis en grænse for, hvor stor en lodret last en given søjle kan optage, selv uden samtidig momentpåvirkning. Hvis den lodrette last nærmer sig denne grænse, bliver der mindre og mindre overskud til momentpåvirkningen.

Når diagrammet her benævnes n-m-diagram og ikke N-M-diagram skyldes det, at diagrammet viser lodret last pr. længdeenhed og moment pr. længdeenhed, og ikke samlet lodret last og moment på hele væggen. Diagrammet konstrueres efter Ritterformlen.

Den aktuelle kombination af lodret last og moment bestemmes under hensyntagen til

• Den lodrette last på toppen af væggen
• Egenlasten af væggens øverste del
• Væggens topexcentricitet e₀ og dens eventuelle bundexcentricitet
• Væggens afvigelse fra planhed e₅
• Væggens tværlast

Programmet bestemmer lodret last og moment i en række snit i søjlens midterste trediedel og udvælger det snit, hvori momentet er størst, som det dimensionsgivende. Kombinationen af lodret last og moment i dette snit sammenlignes derefter med n-m-diagrammet.

 

Automatisk reduktion af materialeparametre ved små tværsnit

Hvis væggens tværsnitsareal er mindre end 0,10 m², skal der regnes med reducerede styrker og E-modul.

Hvis tjekmærket er sat ved "Automatisk reduktion ...", og hvis væggens tværsnitsareal er mindre end 0,10 m², reducerer programmet tryk- og vedhæftningsstyrkerne samt E-modulet med reduktionsfaktoren

• R₁ = 0,7 + 3 × A

Det forudsættes, at der er angivet "normale" styrkeparametre (uden reduktion for små tværsnit), og at der anvendes byggesten med indmuringsmål > 0,05 m² (fx alm. mursten).

Hvis der anvendes blokke med indmuringsmål > 0,05 m², og væggens tværsnitsareal højst svarer til 2 blokke, skal der anvendes en anden reduktionsfaktor

• R₂ = 0,7 + 0,15 × n

Denne formel er ikke indbygget i programmet, så her må brugeren selv beregne de reducerede styrkeparametre og angive dem i de relevante felter, samt fjerne tjekmærket ved "Automatisk reduktion ...".

 

Densitet

Værdien overføres automatisk fra fanebladet Murværk, men kan overskrives for den aktuelle komponent.

I flere moduler bestemmes væggens egenlast pr. m² vægflade som densiteten gange vægtykkelsen. Hvis et evt. pudslag ønskes medregnet til egenlasten, må densiteten sættes tilsvarende højere, idet vægtykkelsen af hensyn til bæreevnen ikke må angives med en for stor værdi.

 

Topexcentricitet e₀

Den lodrette last forudsættes normalt at angribe toppen af væggen excentrisk. Et indspændingsmoment i et tværsnit omregnes til en excentricitet ved division med den lodrette last i tværsnittet. Størrelsen af e₀ afhænger af, hvorledes den lodrette last påføres, altså hvordan detaljerne ved væggens top er udformet. Hvis lasten rent fysisk kan angribe over hele tværsnittet, anvendes ofte e₀ = e_d/6, svarende til, at den lodrette last er trekantformet fordelt over hele tværsnittet med trykspændingen 0 i den ene side af tværsnittet.

Topexcentriciteten måles fra midten af tværsnittet til den lodrette lasts resultant ved væggens top, og den er positiv, hvis den lodrette last står til højre for tværsnittets midte, Den regnes altså positiv modsat tværlastens retning. Hvis f.eks. den aktuelle væg er en ydervæg med udvendigt sug og indvendigt overtryk, og hvis lastresultanten angriber 18 mm fra væggens midte ind mod husets indre, er e₀ = 18 mm, altså positiv.

I en kombinationsvæg optræder der normalt et supplerende topmoment, som er modsat rettet det "basale topmoment" (Lodret last gange e₀). Det skyldes, at en del af det basale topmoment overføres fra bagvæggen til formuren gennem de øverste binderrækker. Det supplerende topmoment omregnes til en reduktion af e₀ ved division med den lodrette last.

 

Elasticitetsmodul E_0k

Værdien overføres automatisk fra fanebladet Murværk, men kan overskrives for den aktuelle komponent.

 

Planhedsafvigelse e₅

Man kan aldrig regne med, at en muret væg er helt plan. Små afvigelser fra planet forekommer altid i praksis. For en etagehøj mur med højde indtil 3,4 m gælder, at murens pilhøjde regnet fra forbindelseslinien mellem fodpunkt og toppunkt højst må være 10 mm. Den normale værdi for e₅ er derfor 10 mm, men hvis man i projektet kræver at afvigelsen er mindre, og hvis man kontrollerer på byggepladsen, at det opfyldes, kan man indtaste en tilsvarende mindre værdi.

Der indtastes altid en positiv værdi for e₅. Programmet gennemregner væggen for begge situationer, altså både for e₅ i tværlastens retning, og for e₅ modsat tværlastens retning.

 

Fodreaktion må regnes excentrisk

Der tages hensyn til indspændingsgraden for dæk eller bjælker ved bestemmelse af excentriciteterne.

En muret væg, der står på et stift dæk, kan tilsvarende regnes indspændt ved væggens fod. En ydervæg, der står på et ueftergiveligt fundament og påvirkes af vindtryk udefra, vil bøje lidt indad, og væggens nederste del vil rotere lidt. Dette vil medføre, at reaktionen ved væggens fod rykker indad, således at der optræder en slags indspændingsmoment ved væggens fod. Dette forhold virker til gunst for væggens bæreevne, idet momentet fra vinden ved væggens midte reduceres. e_0,bund kan maksimalt sættes til t/6 når muren placeres på et stift fundament.

Hvis en væg står på et dæk, der bøjer ned som følge af nyttelasten på dækket, samtidig med at væggen bøjer som følge af vindlast, kan det være vanskeligt at vurdere, hvilken vej væggens reaktion eventuelt rykker. I denne situation kan det være rimeligt at benytte den simplificerende antagelse om, at excentriciteten ved væggens fod er nul.

Hvis tjekmærket er sat ud for "Fodreaktion må regnes excentrisk", bestemmer programmet excentriciteten ved væggens fod på grundlag af følgende antagelser:

1. Væggen regnes som en idealelastisk bjælke, indspændt ved foden, simpelt understøttet ved toppen, påvirket af et moment i toppen (lodret last gange e₀) og af den angivne tværlast.
2. Indspændingsmomentet ved foden bestemmes og divideres med reaktionens størrelse (lodret last væggens egenlast).
3. Den herved fundne excentricitet begrænses til 1/6 af vægtykkelsen, således at der ikke optræder trækspændinger eller revner i tværsnittet.

Hvis tjekmærket IKKE er sat ud for "Fodreaktion må regnes excentrisk", regner programmet med, at excentriciteten ved væggens fod er nul.

I begge tilfælde bestemmes derefter den resulterende excentricitet i en række tværsnit i væggens midterste trediedel, idet der tages hensyn til lastexcentriciteterne ved top og bund, tværlasten samt planhedsafvigelsen e₅ (som antages parabelformet). Planhedsafvigelsen kan naturligvis gå i såvel samme som modsat retning af tværlasten. Begge tilfælde undersøges, og det dimensionsgivende tilfælde vises og anvendes.

Den største af disse resulterende excentriciteter, e_t, indgår i bæreevneberegningen.

 

Trykstyrke f_k

Værdien overføres automatisk fra fanebladet Murværk, men kan overskrives for den aktuelle komponent.

 

Bøjningstrækstyrke f_xk1

Værdien overføres automatisk fra fanebladet Murværk, men kan overskrives for den aktuelle komponent.

 

Højde

Højden er principielt afstanden mellem de punkter, hvor udbøjning er forhindret.

Hvis den aktuelle væg står på et dæk eller et fundament, regnes højden fra dækkets eller fundamentets overside.

Hvis den aktuelle væg er understøttet af et dæk, som hviler på væggens overside, regnes højden til undersiden af dækket.

 

Lodret last på væg

Den samlede lodrette last på væggen divideret med væggens effektive længde, dvs væggens samlede længde minus længden af mindre vinduesåbninger etc. Den lodrette lastintensitet uden hensyn til åbninger kan normalt fås fra modulet Lastberegning. Denne lastintensitet skal multipliceres med væggens samlede længde og divideres med væggens effektive længde.

Egenvægten skal ikke medtages i den lodrette last, da denne medtages via densiteten og tykkelsen

En lodret punktlast kan fordeles under 1:2.

Er væggen fx 2,8 m høj kan der for en punktlast øverst på den centrale del af vægfeltet (som er min. 2,8 m / 4 = 0,7 m vandret fra den lodrette kant) regnes med en vandret udstrækning af vægfeltet på: 2 x 1,4 m/2 = 1,4 m.

Er den koncentrerede last beliggende på kanten kan regnes med en vandret udstrækning af vægfeltet på: 1 x 1,4 m/2 = 0,7 m.

I begge tilfælde skal tages hensyn til spaltekræfter, mulighed for vandret modhold i konstruktionen, etc. Disse forhold kan være kritiske.

 

Tværlast (vind)

Tværlasten er næsten altid vindlast, som dels virker direkte på væggen, dels i nogle tilfælde overføres til eller fra væggen via jævnt fordelte bindere. Tværlasten forudsættes ensformigt fordelt over hele væggens areal. Den regnes altid positiv, idet fortegnene for den lodrette lasts excentriciteter defineres i forhold til tværlastens retning.

      

Vandrette mål

Modulet baserer sig på en model, der forudsætter en massiv væg uden åbninger som fx vinduesåbninger. For en bærende væg med åbninger må man derfor regningsmæssigt koncentrere den samlede last på vægfelterne mellem åbningerne. Det kan gøres ved at man multiplicerer den gennemsnitlige linielast på væggen med forholdet mellem den samlede væglængde og summen af længderne af vægfelterne mellem åbningerne.

Ved bestemmelse af søjlelængden for en bærende væg (det "aktuelle" vægfelt) kan der tages hensyn til eventuelle tværvægges afstivende effekt, hvis det aktuelle vægfelt er muret i forbandt med tværvæggene, eller på anden måde er effektivt forbundet dermed. I modsætning til hvad der gælder for overførslen af lodret last som beskrevet ovenfor, så kan et vægfelt med en mindre vinduesåbning antages at være afstivet af de eventuelle tværvægge som en gennemgående væg uden hensyn til vinduesåbningen. Det er op til brugeren at vurdere hvor grænsen går for en mindre vinduesåbning, og om der evt. kan være flere vinduesåbninger i den samme væg.

Det sikres, at tykkelsen overholder eventuelle minimumskrav angivet i det nationale anneks N.A. (ikke aktuelt for DK)

For at en tværvægs afstivende effekt kan tages i regning kræves det, at I_tvær > I_A, hvor I_tvær er tværvæggens inertimoment, og I_A er inertimomentet af den del af det aktuelle vægfelt, som tværvæggen forudsættes at understøtte.

Inertimomenterne skal beregnes om akser i eller parallelt med det aktuelle vægfelts plan. De skal endvidere beregnes på grundlag af regningsmæssige tværsnit, dvs murdimensionerne skal reduceres med eventuelle fugedybder.

Hvis den nævnte betingelse er opfyldt, altså hvis tværvæggen(e) er stiv(e) nok, reduceres søjlelængden. I formlerne indgår væglængden l, som for et firesidigt understøttet vægfelt er afstanden mellem tværvæggene, og for et tresidigt understøttet vægfelt er afstanden fra tværvæg til vægafslutning. Denne længde benævnes i dette modul "A-længden".

Det aktuelle vægfelts tykkelse benævnes "A-tykkelsen", og venstre og højre tværvægs dimensioner benævnes V-længden, V-tykkelsen, H-længden og H-tykkelsen.

Det følgende eksempel viser hvorledes disse mål kan fastsættes.

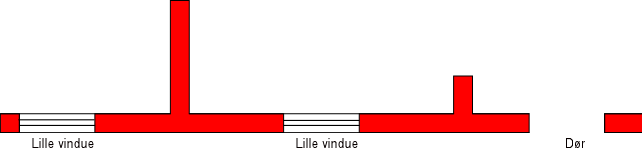
Figur 1. Konstruktion

Den bærende væg og de afstivende tværvægge opdeles i enheder som vist:

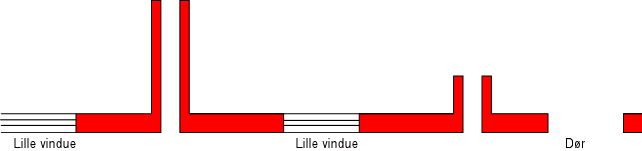
Figur 2. Opdeling

Brugeren vurderer selv, efter hvilket forhold en afstivende tværvægs tykkelse skal fordeles på de to vægdele som den afstiver.

Derefter beregnes hver enhed separat. En enhed ser i princippet således ud:

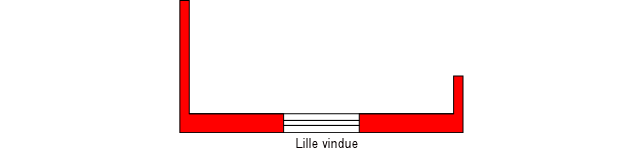
Figur 3. Aktuel vægfelt

Dette er en "fuldt udstyret" væg, men naturligvis kan den ene eller begge afstivende tværvægge mangle. Hvis vinduesåbningen ikke er for stor ses der som nævnt bort fra denne ved bestemmelsen af de afstivende tværvægges effekt. Afstivningsforholdene og den effektive væghøjde kan således bestemmes på basis af følgende data foruden den fysiske væghøjde:

Figur 4. Betegnelser

---