Masonry walls subjected to shear loading
This module design stabilizing walls subjected to in-plane horizontal and vertical loads. Shear walls can be rather complicated to design because areas of fractures are not so easily identified as they are for e.g. plates and beams. The procedure for design are briefly explained below.
The shear capacity between the shear wall and flanges (if any) are determined. The forces are transferred via obliqued (compression)stringers and horizontal tension stringers (wall-ties). The length of the flanges are reduced according to EN 1996 - 1 - 1.The minimum length of the flanges are the thickness of the wall.
The wind load is pressumed coming from left.
Vertical cross-section through the shear wall are investigated. The cross-sections are labelled : A, B, C, D:
- A. cross-section between shear wall and left flange (seam)
- B. Direct left to the area of loading
- C. Direct left to the area of reaction
- D. cross-section between shear wall and right flange (seam)
- At the support: Shear capacity. (Horizontal cross-sections)
- Cross-section B: Vertical fracture in the units. Horizontal fracture in the bed joints. Stringers of tension and compression. (Vertical cross-section)
- Cross-section C: As above supplemented with an analysis regarding the compression stresses. (Vertical cross-section)
- Bed joint above stringers of compression. Shear stresses. (Horizontal cross-sections)
- Bed joint below stringers of tension. As above supplemented with analysis of the excentric load (if any). (Horizontal cross-section)
- Area of loading: Normal- and shear stresses. (Horizontal cross-section)
The limitations for shear stresses are set to 1,5 MPa.
Vertical distance between wall-ties
The distance is given in mm
Typically wall-ties are placed in every 2. or 4. joints in the cross-section between the shear wall and flanges. The forces are transferred via obliqued (compression)stringers and horizontal tension stringers (wall-ties).
Density
The dead load of the shear wall is normally a part of the stabilizing load.
In case of a safety factor smaller than 1,0 the density should be reduced.
Masonry of solid units (group 1):
The density is typically 1700 - 1800 kg/m³
Masonry of cell units (group 2):
Following values can be used:
| Cavity proportion % | Density kg/m³ |
| 10 | 1580 |
| 15 | 1510 |
| 20 | 1440 |
| 25 | 1370 |
| 30 | 1300 |
| 35 | 1230 |
| 40 | 1160 |
The table is based on following assumptions
Density of the units: 1800 kg/m³
Percentage of units: 78,4 %
Density of mortar: 1700 kg/m³
Percentage of joints: 21,6 %
Proportions of not-filled area in the joints: 15 %
Corrections:
Clinker units may have a density of more than 2000 kg/m³
Moler units normally have a density of 500 - 800 kg/m³
In several of the modules the self load of the wall pr m² is calculated by multiplying the density by the thickness. If a plaster coat is to be included in the dead load, the density must be increased accordingly, since the thickness of the wall, in consideration of the load bearing capacity, shouldn't be corrected.
Eccentricity, e0
The eccentricity of the vertical load, perpendicular to the plane of the wall, at the upper side of the wall, is stated.
Each single partial load with its own eccentricity contributes to the resulting load and the resulting eccentricity. Each single partial load's eccentricity must be considered as "large as possible" or as "small as possible", depending on what results in the largest total eccentricity.
A stabilizing wall is not considered to be subject to transverse loading, which implies that the direction of the eccentricity is unimportant, since the wall is symmetrical in its own plane.
In reality the wall is of course subjected to a wind load, which results in the usual moment stress distribution parallel with the head and the bed joints. This stress disribution results in, for the area of compression in the bed joint, an extra contribution to the shear bearing capacity of +µd * σ.
In the tension area the shear bearing capacity is similarly diminished by -µd * σ. In the preceding σ is the compressive normal stress. All in all, the transverse loading is not considered to have any significant influence of the shear bearing capacity.
The horizontal load is considered to have the same eccentricity as the vertical. This is a safe assumption, since a part of the horizontal loads normally are transferred via the unstressed cross section.
For decks placed one sided, e0 is e.g calculated by:
e0 = t/2 - a1/3
Where t is the thickness of the wall, and a1 is the depth of the support for the deck.
Eccentricity in-plane of the wall eL
The moment from the wind load is distributed according to stiffness of the transversing walls. The moment results in an eccentricity of the normal force in the plane of the wall.
The eccentricity is calculated by: eL = M/N
For walls in top floor eL is normally 0 mm.
Compressive strength fk
The value is transferred automatically from the heading "Masonry".
The value can, of course, be overwritten in the current calculation.
Eccentricity e0, flanges
The eccentricity of the vertical load on the upper side of the wall. One of the main principles in this calculation is that each vertical subload, with its own eccentricity, gives a contribution to the resulting load and the resulting eccentricity, and the eccentricity belonging to each individual subload must be assumed to be as "large as possible" or as "small as possible", depending on what gives the largest total eccentricity.
For unilaterally placed floor components, e0 is given by:
e0 = t/2 - a1/3
where t is the walls thickness and a1 is the depth of the support for the deck.
The eccentricity of the vertical load of the flanges, however, has little influence on the bearing capacity of the stabilizing wall.
Effective length of flanges
Maximum distance from the centerline of the shear wall to the nearest vertical free edge or large opening
Large openings are defined as openings with dimensions:h > 1/4 * storey height or
l > 1/4 * length of the shear wall
h, l is the height and length of the opening
If a wall is containing 2 or more small openings, the total area should be less than 1/10 of the area of the wall.
Vertical load on the right flange
The load on the right flange has only little influence on the bearing capacity of the shear wall because the load, for the main part, continues through the flange to the support. The load on the right flange and the specific weight can easily be set equal to zero, due to following considerations.
Transversing partitions are typically made after the floor components are placed on the longitudinal walls. The strain necessary for the absorbance of the force in the longtudinal walls will thereby be present, and the bricking up of the transversing walls will not alter this condition much.
This means that the vertical loads are absorbed directly through the longitudinal walls, and have no real influence on the absorbance of shear stress.
An initial rotation of the stabilizing shear wall will, however, introduce strain in the flange, and thereby a stabilizing shear force in the seam between the flange and the shear wall.Vertical load on the left flange
During the initial rotation, the shear wall will try to "lift" the left flange, which, statically speaking, means that a stabilizing shear force will develop on the shear wall .
The same mecanism will occur for the shear wall on the storey immediately above, which means that the only load affecting the shear wall in question by the "lift", is the dead load of the flange and the load of the floor component of the storey immediately above.
Furthermore, the shear capacity of the seam is often the deciding factor in the design, whereby a heavier load on the flange, only would mean a corresponding reduction of the flange during the calculation.
Thickness
Rules in the N.A. for minimum thickness of walls shall be applied
No reduction is necessary for joint depths less than, or equal to, 3 mm. In cases of joint depths exceeding 3 mm, the thickness should be reduced by the full joint depth.
Example: If the masonry is constructed using wide units (150 mm) with a one-sided recessed joint, with a depth of 10 mm, the thickness should be: 150 mm - 10 mm = 140 mm.
Characteristic anchorage strength of wall ties
The shear force between the flanges and the stabilizing wall is considered to be transferred by a system of stringers, consisting of transversing compressive stringers at an angle of approximately 45 degrees, and horizontal tension stringers in the wall ties.
The tensile strength of the wall ties is set equal to the anchorage strength.
The value is transferred automatically from the module "Masonry". The value can, of course, be overwritten in the current calculation.
Characteristic coefficient of friction µk
Friction, µk, is the part of the shear strength not resulting from the cohesion.
The value can for mortars with cement be set to 1,0. For lime mortars with no cement the value is 0,6. The value is transferred automatically from the heading "Masonry".
The value can, of course, be overwritten in the current calculation.
Characteristic coefficient of friction at the bottom, µk,bottom
The following values can be used for µk,bottom against a damp proofing course:
|
Foundation |
Cardboard | Plastic foil |
| Plane | 0.49 | - |
| Light-weight concrete | 0.44 | 0.62 |
Height
If the shear wall is placed on a floor component or a foundation, the design value of the height is measured from the upper side of the floor component or foundation.
However, if a damp-proof course is placed 2 courses above the foundation, for example, the height is measured from this point.
If the shear wall at the top is horizontal supported by a floor component, resting on the upper side of the wall, the design value of the height is measured to the lower side of the floor component (e.g. a slab).
Shear factor, km
The shear strength for the units is considered proportional with
the compression strength.
If no test results or other documentation is present, the following values can
be used:
| km | = 0.07 for clay |
| = 0.20 for light weight concrete |
Characteristic initial shear strength fvk0
The initial shear strength is the part of the shear strength not resulting from friction.
The value is transferred automatically from the module
"Masonry".
The value can, of course, be overwritten in the current calculation.
Characteristic initial shear strength fvk0,bottom at the bottom
The initial shear strength is the part of the shear strength not resulting from friction.
fvk0,bottom is usually 0 for walls on a damp proofing course.
Length
The shear wall must be made without vertical tongue joints, expansion joints, and without larger openings. (At the ends a free edge or vertical tongue joints are expected)
Head joint 1 : n
The vertical shear capacity is calculated in the cross section that runs through the maximum amount of head joints.
To calculate the effective cross section, the distance between head joints directly above each other, is indicated in the fraction 1:n.Out of e.g. 4 courses will 3/4 be the effective cross section when n = 4.
The following values are typical:
| n | Bond pattern |
| 2 | ¼ stone running bond |
| 2 | ½ stone running bond |
| 2 | Running bond I |
| 4 | Running bond II |
| 2 | Monk bond |
| 2 | Cross bond |
| 2 | Block bond |
It is conservative to set the value s = 2
Vertical load
The design value of the vertical load is the sum of the design value of the loads from the floor components, etc. above, directly influencing the shear wall. The vertical load usually works in favour of the stability and should only be the dead load. The vertical load is applied at the top, as a concentrated load, in the line of application.
Horizontal load
The sum of the horizontal wind or equivalent earthquake load is distributed by stiffness on the stabilizing walls.
It is not possible to induce an evenly distributed, horizontal, local load on the left, vertical edge. Half of such a load could be included in the vertical load at the top. The rest of the load can be seen as applying to the bottom. If sliding is critical the total load should be applied on the top.
The capacity of the tension stringer
To create equilibrium in an area of shear for the stresses present, it is necessary to introduce a tension stringer in the upper side. The tension stringer can consist of a stringer of wood, joint reinforcement in the deck casting, embedded reinforcement in the joints, or the masonry's own tension bearing capacity.
wooden plank:
A tension stringer can not consist of a wooden plank nailed into a AAC wall.
A tension stringer can possible consist of a wooden plank screwed into a masonry wall. The sum of the anchorage of the screws should be equivalent to the total force in the tension stringer in a certain distance. This phenomenon is illustrated on the figure below The "capacity of the tension stringer" should not be larger than the total anchorage of the screws for a distance equivalent to minimum (L/2; 2 m) where L is the length of the stabilizing wall.
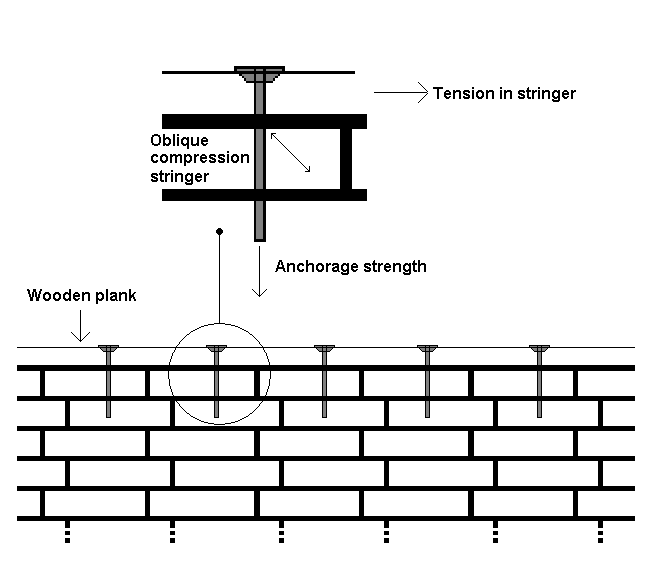
Figure 1. Masonry wall- wooden plank - solution
Reinforcement:
Example: 1Ø8 mm reinforcement bar with fyd = 161 MPa is placed in the deck casting. A 2 * 5 mm reinforcement system with fyd = 464 MPa is placed in the uppermost bed joint. This gives:
Ts = π/4 * (2 * 5² * 464 + 8² * 161)/1000 = 26,31 kN
Tension strength of the masonry:
If no tension stringer is placed, the tension bearing capacity of the
masonry can be applied. The value depends on the bond type, the shear strength,
and the tensile strength of the units.
Following expression can be used:
Ts = Minimum ((0,14 * sqrt(fb) * h * b * n), (µd * σ + fvd0) * b * sl))
Where:
0.14 * (fb)½ represents the tensile strength of the units in MPa
h, b is the height and width of the units
n is the amount of units in the cross section that pass the largest possible amount of head joints (in the 5 uppermost courses).
µd, σ is the design friction and the normal stress in the courses
fvd0 is the design initial shear strength
sl is the smallest total length of bed joints subject to shear failure, when the 5 uppermost courses are subjected to a tensile fracture.
The first part of the expression represents a tensile fracture through the units. The second part represents a zig-zag fracture through the joints alone. The tensile capacity of the head joints is assumed to be nil. The lowest value is to be used.
A shear wall not subjected to any load (σ = 0), with a bond pattern with aligning head joints in every other course (n = 2) has the lowest bearing capacity.
Ts = 2.4 kN for masonry t = 100 mm
Compressive strength fb
The compressive strength for a given type of unit is supplied by the producer.