Vertical loaded wall (Ritter)
Determination of load capacity for a vertical loaded wall without openings according to the Ritter method. The wall may have a horizontal load as well.
The Ritter formula is not mentioned in EN 1996 – 1 – 1 and is an alternative method, described below:
Since the load is a combination of vertical load, horizontal load and moments of eccentricity, the load capacity is not a given value, but a mn-diagram. The section forces from the actual load-combination should be “inside” the mn-diagram giving a sufficient load capacity.
A mn-diagram for a column gives the relation between a vertical load and a corresponding moment. For a column designed by a material without flexural strength there can’t exist a “moment” without a corresponding vertical load to stabilize the column.
The load-capacity is calculated in 2 states (the un-cracked and the cracked phase).
In the un-cracked phase the flexural strength is taking into consideration. The mn-diagram is developed from a straight line from the point of "pure bending" to the value in the mn-diagram (cracked phase) corrrosponding to the eccentricity t/6.
In the cracked phase the flexural strength is assumed to be zero. The mn-diagram is constructed from the Ritter formula. The section forces (= actual value for m and n) should be inside the combined curves.
The actual combination of vertical load and moment is determined from:
- The vertical load on the top of the wall
- The dead load in the upper part of the wall
- Eccentricity in top and bottom
- Out of plane deviation of the wall
- Horizontal load
The program determine combinations of vertical load and moment in different cross-sections and selects the cross-section with the largest moment as the design value. The combination of vertical load and moment is then compared with the mn-diagram’s.
Automatic reduction of parameters of strength for small cross sections
According to EN 1996 - 1 - 1 the compressive strength shall be reduced in case the cross-section < 0,10 m2. In this module all parameters of strength are reduced.
If automatic reduction is marked and the cross-section < 0,10 m2 the program will perform the reduction:
R1 = 0,7 + 3 × A
Density
The value is transferred through the heading “Masonry”. The value can be overwritten.
In several modules the dead load of the wall pr square meter is determined as the density multiplied the wall thickness. If any rendering should be added to the dead load, the density should be corrected (e.g set 10 % higher to include the render). The thickness should be exact, thus giving the “exact” load capacity.
Topeccentricity e0
e0 is the eccentricity in top of wall, positive to the right. The users determine the total eccentricity in case the vertical loads consist of several contributions (e.g. slab to the left and right and a wall in top).
Characteristic module of elasticity E0k
The 5 % fractile is stated
The value is transferred through the heading “Masonry”. The value can be overwritten.
The results from recently performed research gives: E0k:
E0k = min(1000, 400*fm, 20*fb) x fk for mortar with cement (and lime)
E0k = 150*fm x fk for mortar with only lime
In case fm < 1,0 MPa the mortar will be regarded as "pure" lime-mortar. (Note, mark (ML)" in the input field "Method" in the heading "Masonry" when the content of lime > 50% of the binder)
Out-of-plane eccentricity e5
When using the Ritter method for determining the vertical load capacity, e5 is the out-of-plane-eccentricity for the wall. The parameter presumes a certain curvature of the wall (parabolic) and the value represent the maximum deflection in the middle. The parameter is not quite similar to einit in EN 1996 - 1 - 1, because the "deflection" einit can be in full height
Eccentric reaction at the footing
The support condition at the footing can be regarded as simple (no moment can be transferred = equal to nil eccentricity) or with an eccentric reaction giving a moment in favour for the construction. The eccentricity is set to maximum t/6. The actual value is determined through an elastic calculation.
Compressive strength, fk
The value is transferred automatically from the heading "Masonry". The value can, of course, be overwritten in the current calculation.
Flexural strength fxk1
The characteristic flexural strength of masonry having the plane of failure parallel to the bed joints.
The value is transferred automatically from the heading "Masonry". The value can, of course, be overwritten in the current calculation.
Height
If the wall is placed on a slab or a foundation, the height is measured from the top of the slab or foundation.
If the wall at the top is horizontal supported by a floor component, resting on the upper side of the wall, the design value of the height is measured to the lower side of the floor component (e.g. a slab).
Vertical load
The assumptions for the calculation in this module are a wall supported at the top and bottom and without openings. The load at the top of the wall shall be corrected for openings if any. This shall be done geometrically. E.g for a 6,0 m long wall with 2 openings each with a width of 1,0 m the vertical load shall be increased a factor: 6/(6-4) = 1,5. This correction gives a more correct load in the middle height where the failure will occur. The vertical load can normally be extracted from the module “calculation of loads”
The dead load of the wall shall not be implemented in the value. The dead load is calculated via the density and thickness
A vertical point load can be distributed in 1:2. The height of the wall is e.g 2,8 m. A point load at the top on the central part of the wall (central part = minimum 2,8 m / 4 = 0,7 m horizontal from a vertical edge) can be regarded as having a horizontal extension in the wall of: 2 x 1,4 m/2 = 1,4 m.
Is the concentrated load direct on the vertical edge the horizontal extension in the wall can be estimated to: 1 x 1,4 m/2 = 0,7 m.
In both situations vertical split-forces shall be thoroughly examinated.
Horizontal load
This load is practically always wind load, either directly acting on the exposed wall or through the evenly distributed wall-ties. The value is always positive (going to the left). The eccentricity for the vertical load can be positive or negative and thus acting in the same or opposite direction of the wind load.
Horizontal dimensions
The effective height can be reduced when the wall has one or two vertical supports in the ends.
These supporting walls consist typically of walls perpendicular on the wall regarded and they can support more than the actual wall, typically a continuation of the actual wall. These supporting walls can be split arbitrarily between the walls they support. See sketch below, where
- L is the supporting wall to the left
- R is the supporting wall to the right
- A is the actual wall to be supported
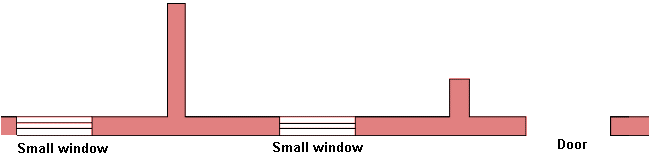
Figure 1. Construction
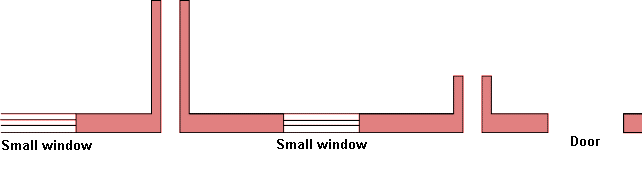
Figure 2. Split of vertical supporting walls
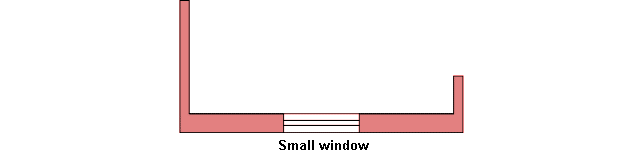
Figure 3. Wall to be designed
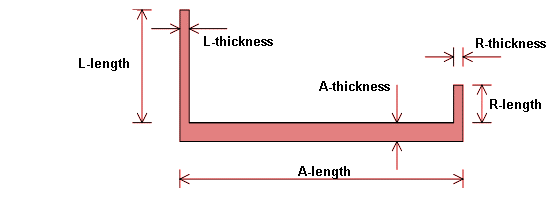
Figure 4. Designations